Introduction #

This tutorial is part of a collection tutorials on basic data structures and algorithms that are created using Kotlin. This project is useful if you are trying to get more fluency in Kotlin or need a refresher to do interview prep for software engineering roles.

How to run this project #

You can get the code for this and all the other tutorials in this collection from this github repo. Here’s a screen capture of project in this repo in action.

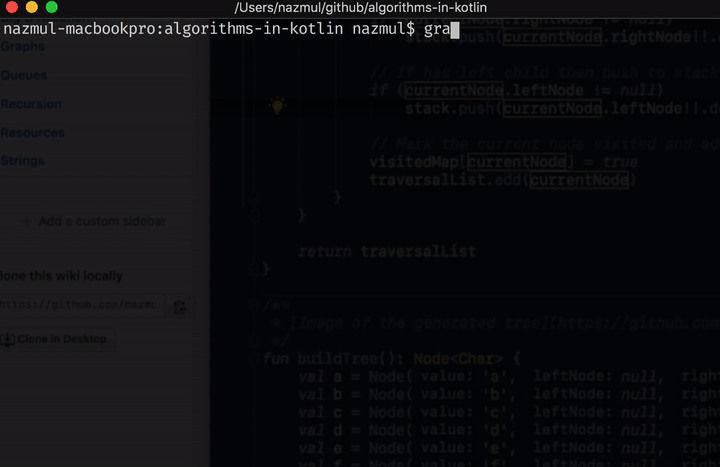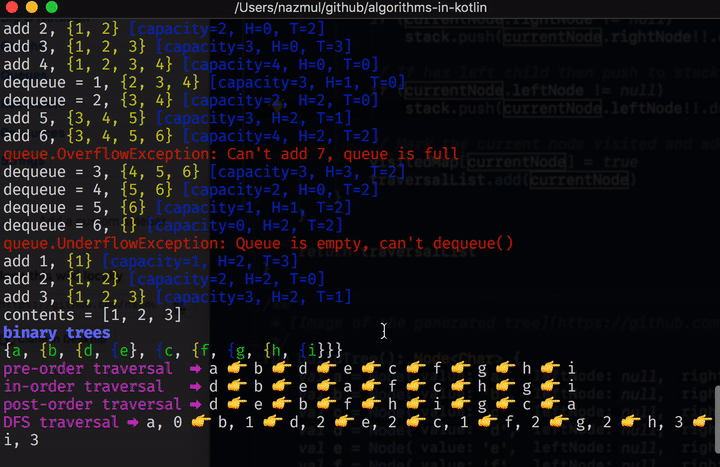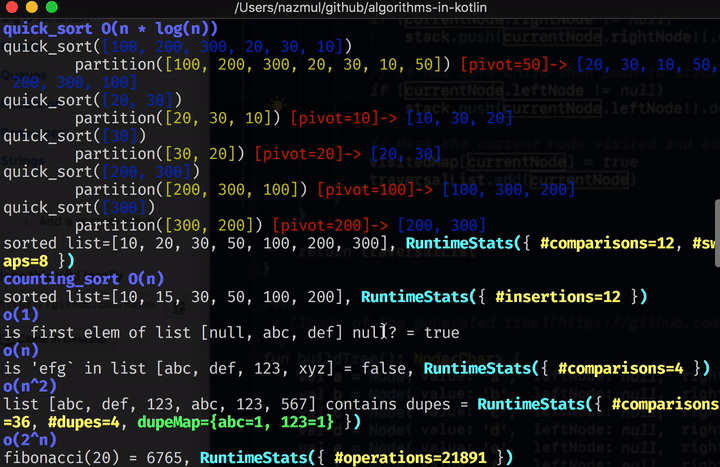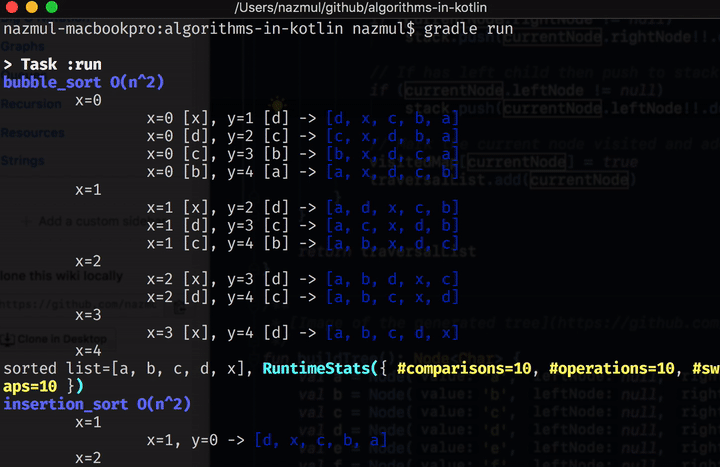
Once you’ve cloned the repo, type ./gradlew run in order to build and run this project from the command line.

Importing this project into JetBrains IntelliJ IDEA #

  • This project was created using JetBrains Idea as a Gradle and Kotlin project (more info). - When you import this project into Idea as a Gradle project, make sure not to check “Offline work” (which if checked, won’t allow the gradle dependencies to be downloaded). - As of Jun 24 2018, Java 10 doesn’t work w/ this gradle distribution (v4.4.x), so you can use Java 9 or 8, or upgrade to a newer version of gradle (4.8+).

Queues and stacks #

Depth first traversal / search #

File systems on computers have a hierarchical file system. Searching for a folder by name is a very common thing to do on computers. On Unix machines, we can use the find -name "somefile" command. How would you implement this command? This is where DFS come into play!

Here’s a simple representation of folders in a hierarchical file system.

class Folder {
    val name: String

    private var _subFolders: MutableList<Folder> = mutableListOf()
    val subFolders: MutableList<Folder>
        get() = Collections.unmodifiableList(_subFolders)

    fun toDetailedString(): String {
        return "{name: $name, subFolders: ${subFolders.size}}"
    }

    override fun toString(): String {
        return name
    }

    fun isNamed(nameArg: String): Boolean {
        return name == nameArg
    }

    constructor(name: String) {
        this.name = name
    }

    constructor(name: String, root: Folder) {
        this.name = name
        root.addSubfolder(this)
    }

    fun addSubfolders(vararg folders: Folder) {
        folders.forEach { addSubfolder(it) }
    }

    fun addSubfolder(f: Folder) {
        if (!_subFolders.contains(f)) {
            _subFolders.add(f)
        }
    }

    fun hasSubfolders(): Boolean {
        return !_subFolders.isEmpty()
    }

}

Here’s a function that creates a set of nested folders that we can search.

/*
Create a tree of folders that need to be searched.

    root
      + opt
        + chrome
      + apps
        + idea
        + androidstudio
      + dev
        + java
          + jdk8
          + jdk11

*/
fun makeSampleFolders(): Folder {
    val root = Folder("root")

    val opt = Folder("opt", root)
    val apps = Folder("apps", root)
    val dev = Folder("dev", root)

    val apps_idea = Folder("idea", apps)
    val apps_as = Folder("androidstudio", apps)

    val opt_chrome = Folder("chrome", opt)

    val dev_java = Folder("java", dev)
    val dev_java_jdk8 = Folder("jdk8", dev_java)
    val dev_java_jdk11 = Folder("jdk11", dev_java)

    return root
}

And here’s an implementation of DFS for this example.

fun dfs(name: String, root: Folder): Boolean {
    val stack = ArrayDeque<Folder>()
    stack.push(root)
    var found = false
    while (stack.isNotEmpty()) {
        println("\n...while loop start... ".brightWhite() + "stack=$stack".brightCyan())
        val currentFolder = stack.pop()
        println("👆️️popped: " + currentFolder.toDetailedString().red())
        if (currentFolder.isNamed(name)) {
            found = true
            println("\tfound a matching folder")
        }
        for (f in currentFolder.subFolders) {
            stack.push(f)
            println("👇️push: " + f.toDetailedString().green())
        }
    }
    return found

}

Implementation notes #

  • When sub folders are added to the stack, they are pulled out in reverse order. So if the insertion order is opt -> apps -> dev, then they will be retrieved in reverse order dev -> apps -> opt.
  • The nature of the stack (the last folder added will be the first one retrieved in the while loop) makes the algorithm favor going “deeper” (or depth first, instead of breadth first). The last folder that’s added will be the first one that’s checked at the next iteration of the while loop. And its sub folders will be added to the stack. Repeat this and you have a depth first bias in folder traversal.
  • Once a depth first path is exhausted (by reaching as far as it will go) then the algorithm back tracks, due to the nature of the stack. When dev path has been exhausted, then the next folder to embark upon (for the while loop) is the apps folder. When apps is exhausted, then back tracking via the stack, takes us to opt.

Here’s output from the code itself that highlights this in action for bfs("jdk11", makeSampleFolders()).

Stacks & Queues

...while loop start... stack=[root]
👆️️popped: {name: root, subFolders: 3}
👇️push: {name: opt, subFolders: 1}
👇️push: {name: apps, subFolders: 2}
👇️push: {name: dev, subFolders: 1}

...while loop start... stack=[dev, apps, opt]
👆️️popped: {name: dev, subFolders: 1}
👇️push: {name: java, subFolders: 2}

...while loop start... stack=[java, apps, opt]
👆️️popped: {name: java, subFolders: 2}
👇️push: {name: jdk8, subFolders: 0}
👇️push: {name: jdk11, subFolders: 0}

...while loop start... stack=[jdk11, jdk8, apps, opt]
👆️️popped: {name: jdk11, subFolders: 0}
	found a matching folder

...while loop start... stack=[jdk8, apps, opt]
👆️️popped: {name: jdk8, subFolders: 0}

...while loop start... stack=[apps, opt]
👆️️popped: {name: apps, subFolders: 2}
👇️push: {name: idea, subFolders: 0}
👇️push: {name: androidstudio, subFolders: 0}

...while loop start... stack=[androidstudio, idea, opt]
👆️️popped: {name: androidstudio, subFolders: 0}

...while loop start... stack=[idea, opt]
👆️️popped: {name: idea, subFolders: 0}

...while loop start... stack=[opt]
👆️️popped: {name: opt, subFolders: 1}
👇️push: {name: chrome, subFolders: 0}

...while loop start... stack=[chrome]
👆️️popped: {name: chrome, subFolders: 0}

jdk11 found: true

Breadth first traversal / search #

By replacing the stack in the example above w/ a queue, we end up w/ depth first search. Unlike the stack, which favors folder traversal to happen depth first (since the last item added to the stack is the first one that’s processed, and when a path is exhausted it backtracks to the previously added folder), a queue favors the first folder added to be processed. This results in a totally different behavior from the stack when we traverse our folder tree.

Ring Buffer #

The ring buffer is a queue abstract data type that’s implemented using a fixed size array. This makes it performant with additions and deletions from a runtime and memory standpoint.

The following is an implementation of it in Kotlin.

/**
 * RingBuffer uses a fixed length array to implement a queue, where,
 * - [tail] Items are added to the tail
 * - [head] Items are removed from the head
 * - [capacity] Keeps track of how many items are currently in the queue
 */
class RingBuffer<T>(val maxSize: Int = 10) {
    val array = mutableListOf<T?>().apply {
        for (index in 0 until maxSize) {
            add(null)
        }
    }

    // Head - remove from the head (read index)
    var head = 0

    // Tail - add to the tail (write index)
    var tail = 0

    // How many items are currently in the queue
    var capacity = 0

    fun clear() {
        head = 0
        tail = 0
    }

    fun enqueue(item: T): RingBuffer<T> {
        // Check if there's space before attempting to add the item
        if (capacity == maxSize) throw OverflowException(
            "Can't add $item, queue is full")

        array[tail] = item
        // Loop around to the start of the array if there's a need for it
        tail = (tail + 1) % maxSize
        capacity++

        return this
    }

    fun dequeue(): T? {
        // Check if queue is empty before attempting to remove the item
        if (capacity == 0) throw UnderflowException(
            "Queue is empty, can't dequeue()")

        val result = array[head]
        // Loop around to the start of the array if there's a need for it
        head = (head + 1) % maxSize
        capacity--

        return result
    }

    fun peek(): T? = array[head]

    /**
     * - Ordinarily, T > H ([isNormal]).
     * - However, when the queue loops over, then T < H ([isFlipped]).
     */
    fun isNormal(): Boolean {
        return tail > head
    }

    fun isFlipped(): Boolean {
        return tail < head
    }

    override fun toString(): String = StringBuilder().apply {
        this.append(contents().joinToString(", ", "{", "}").yellow())
        this.append(" [capacity=$capacity, H=$head, T=$tail]".blue())
    }.toString()

    fun contents(): MutableList<T?> {
        return mutableListOf<T?>().apply {
            var itemCount = capacity
            var readIndex = head
            while (itemCount > 0) {
                add(array[readIndex])
                readIndex = (readIndex + 1) % maxSize
                itemCount--
            }
        }
    }

}

class OverflowException(msg: String) : RuntimeException(msg)
class UnderflowException(msg: String) : RuntimeException(msg)

Implementation notes #

  • Since the array is re-used for insertions and deletions, it becomes important to be able to track the usage or capacity of the array (as items are added and removed). This capacity is used to determine whether the array is full or empty, and is used to iterate thru the elements of the array if needed.
  • In order to cycle around the array, the head and tail indices are updated such that when they hit the “end” of the array, they “flip” over. This means that when head reaches maxSize + 1, it just goes to 0. This can be achieved easily by using the % operator. tail = (tail+1) % maxSize is the equivalent of if (tail == maxSize) tail = 0.
  • In order to get all the elements out of the array (as a list) the capacity and the head (or read index) is used in order to get all the elements out as we would expect (which isn’t necessarily how they are laid out in the array).

Resources #

Resources #

CS Fundamentals #

Data Structures #

Math #

Big-O Notation #

Kotlin #

Markdown utilities #

#cs #kt
👀 Watch Rust 🦀 live coding videos on our YouTube Channel.



📦 Install our useful Rust command line apps using cargo install r3bl-cmdr (they are from the r3bl-open-core project):
  • 🐱giti: run interactive git commands with confidence in your terminal
  • 🦜edi: edit Markdown with style in your terminal

giti in action

edi in action

Related Posts