Introduction #

This tutorial is part of a collection tutorials on basic data structures and algorithms that are created using Kotlin. This project is useful if you are trying to get more fluency in Kotlin or need a refresher to do interview prep for software engineering roles.

How to run this project #

You can get the code for this and all the other tutorials in this collection from this github repo. Here’s a screen capture of project in this repo in action.

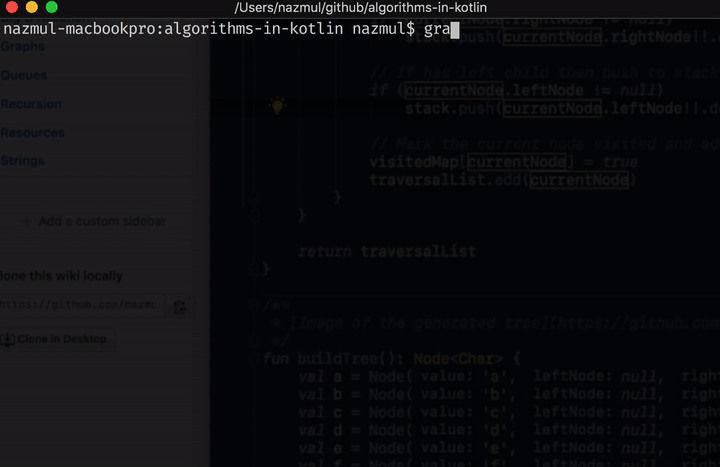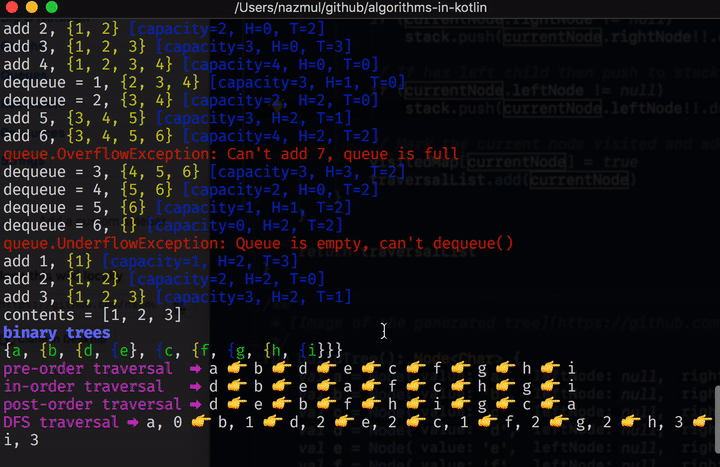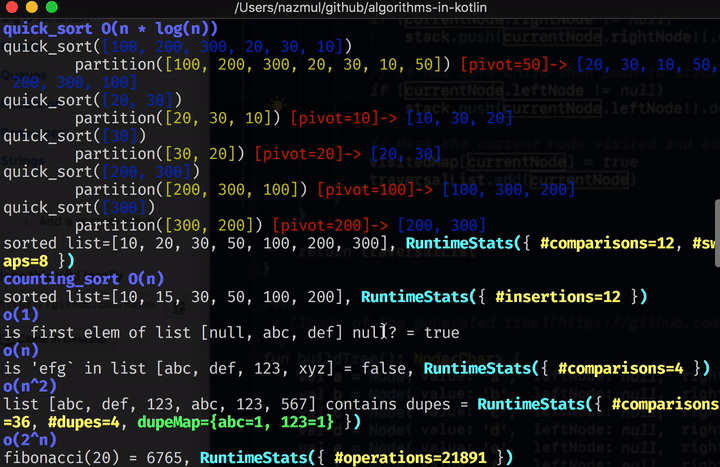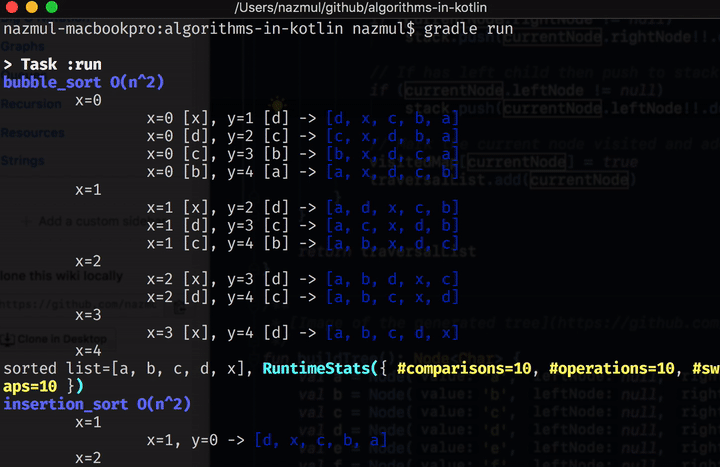
Once you’ve cloned the repo, type ./gradlew run in order to build and run this project from the command line.

Importing this project into JetBrains IntelliJ IDEA #

  • This project was created using JetBrains Idea as a Gradle and Kotlin project (more info). - When you import this project into Idea as a Gradle project, make sure not to check “Offline work” (which if checked, won’t allow the gradle dependencies to be downloaded). - As of Jun 24 2018, Java 10 doesn’t work w/ this gradle distribution (v4.4.x), so you can use Java 9 or 8, or upgrade to a newer version of gradle (4.8+).

Induction #

Let’s use an example to illustrate induction. Let’s say that you have a bunch of coins of fixed denominations. And you’re tasked with figuring out the fewest coins that you would need to put together in order to arrive at some total amount. Let’s say you have denominations of 1, 5, 7, 11 and you’re asked to see how few coins you can select in order to get a total of 49.

Brute force approach #

Using the brute force approach you could simply see how many 11 denomination coins would get you close to the total. There would be a remainder (4 x 11 denomination coins = 44). Then you could see how many 7 denomination coins fit. And so on with 5 and 1 denomination coins. You could write this up in the following code.

/**
 * Brute force version of the recursive function [numCoins] above.
 *
 * - As you can see, there's a lot more code and complexity to compensate
 *   for very simplistic logic.
 * - The coin denominations are hard coded to be 1, 5, 7, 11.
 */
fun numCoins_nonrecursive(total: Int, coins: Coins) {
    // Exit condition.
    if (total == 0) return

    var currencyRemoved = 0

    // Remove all the 11 coins.
    val numberOf11s = (total / 11)
    if (numberOf11s > 0) {
        coins.numberOf11s += numberOf11s
        currencyRemoved += numberOf11s * 11
    }

    // Remove all the 7 coins.
    val numberOf7s = (total - currencyRemoved) / 7
    if (numberOf7s > 0) {
        coins.numberOf7s += numberOf7s
        currencyRemoved += numberOf7s * 7
    }

    // Remove all the 5 coins.
    val numberOf5s = (total - currencyRemoved) / 5
    if (numberOf5s > 0) {
        coins.numberOf5s += numberOf5s
        currencyRemoved += numberOf5s * 5
    }

    // Remove all the 1 coins.
    val numberOf1s = (total - currencyRemoved) / 1
    if (numberOf1s > 0) {
        coins.numberOf1s += numberOf1s
        currencyRemoved += numberOf1s * 1
    }

}

data class Coins(var numberOf1s: Int = 0,
                 var numberOf5s: Int = 0,
                 var numberOf7s: Int = 0,
                 var numberOf11s: Int = 0) {
    override fun toString() = StringBuilder().apply {
        val result = mutableListOf<String>()
        arrayOf(::numberOf1s, ::numberOf5s, ::numberOf7s, ::numberOf11s)
            .forEach {
                if (it.get() > 0)
                    result.add("#${it.name} coins = ${it.get()}")
            }
        append(result.joinToString(", ", "{", "}").brightBlue())
    }.toString()
}

Recursion and breaking down the problem #

The brute force approach produced a lot of code. And the denominations of the coins that we can use are hardcoded. This isn’t a good solution. Instead if we use induction and implement it with recursion, then we can do the following.

  1. Come up with the simplest case that we can solve for (that will not require recursion).
  2. Figure out a way to call the function that you’re writing w/ arguments that represent a smaller subset of the problem and use the return value from the function to assemble the final result (whatever that may be).
    • This usually entails performing some logic and then generating new arguments for the same function, that break the problem down into smaller problems.
    • Calls need to be made to the function (recursively) and the result from these calls need to be combined into a final result somehow.

Using this approach this is what the code might look like for the minimum number of coins problem.

/**
 * Use the process of induction to figure the min number of coins it takes
 * to come up with the given [total]. The coin denominations you can used
 * are in [denominations]; this list must be sorted already (in descending
 * order), eg: [11, 7, 5, 1].
 * [coinsUsedMap] has keys that represent the denomination, and value that
 * represent the number of coins used of that denomination.
 */
fun numCoins(total: Int,
             denominations: List<Int>,
             coinsUsedMap: MutableMap<Int, Int>): Int {
    // Show the function call stack.
    println("\tnumCoins(total=$total, denominations=$denominations)".brightYellow())

    // Stop recursion when these simple exit conditions are met.
    if (total == 0) return 0
    if (denominations.isEmpty()) return 0

    // Breakdown the problem further.
    val coinDenomination = denominations[0]
    val coinsUsed = total / coinDenomination

    // Remember how many coins of which denomination are used.
    if (coinsUsed > 0) coinsUsedMap.computeIfAbsent(coinDenomination) { coinsUsed }

    // Breakdown the problem into smaller chunk using recursion.
    return coinsUsed +
        numCoins(total = total - coinsUsed * coinDenomination,
                 denominations = denominations.subList(1, denominations.size),
                 coinsUsedMap = coinsUsedMap)
}

Other examples of using recursion #

Quick Sort #

You can apply the steps above (simplest case, perform logic, split arguments into smaller subset of the problem) to many other examples, such as quick sort.

/** O(n * log(n)) */
fun quick_sort(list: MutableList<Int>,
               startIndex: Int = 0,
               endIndex: Int = list.size - 1) {
    if (startIndex < endIndex) {
        // Perform some logic to break down the problem
        val pivotIndex = partition(list, startIndex, endIndex)

        // Recurse before pivot index
        quick_sort(list, startIndex, pivotIndex - 1)

        // Recurse after pivot index
        quick_sort(list, pivotIndex + 1, endIndex)
    }
}

/**
 * This function takes last element as pivot, places the pivot
 * element at its correct position in sorted list, and places
 * all smaller (smaller than pivot) to left of pivot and all greater
 * elements to right of pivot
 */
fun partition(list: MutableList<Int>,
              startIndex: Int = 0,
              endIndex: Int = list.size - 1): Int {
    // Element to be placed at the correct position in the list
    val pivotValue = list[endIndex]

    // Index of smaller element
    var smallerElementIndex = startIndex

    // Make a single pass through the list
    for (index in startIndex until endIndex) {
        // If current element is smaller than equal to pivotValue
        // then swap it w/ the element at smallerElementIndex
        val valueAtIndex = list[index]
        if (valueAtIndex < pivotValue) {
            list.swap(smallerElementIndex, index)
            smallerElementIndex++
        }
    }

    // Finally move the pivotValue into the right place on the list
    list.swap(smallerElementIndex, endIndex)

    // Return the index just after where the pivot value ended up
    return smallerElementIndex
}

fun MutableList<Int>.swap(index1: Int, index2: Int) {
    val tmp = this[index1] // 'this' corresponds to the list
    this[index1] = this[index2]
    this[index2] = tmp
}

fun binarySearch(item: String, list: List<String>): Boolean {
    // Exit conditions (base cases)
    if (list.isEmpty()) {
        return false
    }

    // Setup probe
    val size = list.size
    val probeIndex = size / 2
    val probeItem = list[probeIndex]

    // Does the probe match? If not, split and recurse
    when {
        item == probeItem -> return true
        item < probeItem -> return binarySearch(item,
                                                list.subList(0, probeIndex),
                                                stats)
        else -> return binarySearch(item,
                                    list.subList(probeIndex + 1, size),
                                    stats)
    }
}

Resources #

CS Fundamentals #

Data Structures #

Math #

Big-O Notation #

Kotlin #

Markdown utilities #

#cs #kt
👀 Watch Rust 🦀 live coding videos on our YouTube Channel.



📦 Install our useful Rust command line apps using cargo install r3bl-cmdr (they are from the r3bl-open-core project):
  • 🐱giti: run interactive git commands with confidence in your terminal
  • 🦜edi: edit Markdown with style in your terminal

giti in action

edi in action

Related Posts